Understanding Lyapunov Functions

August 11, 2024
By Aathreya Kadambi

To explain the photo, I was flying, and I just wanted to point out how confusing these baggage tags are. Just look at this one:

Text that says “Peel here” that has “DO NOT PEEL” directly above it
with three big arrows pointing towards “Peel here”.

😩 It’s actually impossible to put these baggage tags on your bags, I’m telling you. After a long period of thought where I noticed that you could either do it as a sort of Mobius strip or just a regular cylindric shell thingy, I finally got it on. On other confusing things, check out this article on how to write good captions, yet none of the numerous images in the article have any captions in the traditional sense: https://www.schoolwebmasters.com/how-to-write-a-caption. It’s actually a good and thorough article. But really what I was trying to figure out was whether or not I should start off my caption with “Caption:” or “Figure:” or just start it off by writing what I had to say. I still don’t know, but I’ve been told my flight is boarding in less than an hour, so I’m trying to finish this post. 🥶 Edit: I ended up taking a bit longer anyway hehe.

Anyways, I decided I needed to study Lyapunov functions, since I heard that they can be useful in showing existence and uniqueness! I’ll take this opportunity to make a blog post, and maybe tomorrow I’ll make some notes!

Resources

Here are the resources I’m looked at to study Lyapunov functions:

• Of course, the Wikipedia article.
  • This one wasn’t really clear to me to be honest. It was really hard to read and I didn’t understand it much.
• Two great YouTube videos: here and here (there was another one in the playlist between these two)
  • These made a lot more sense to me. Still though, I didn’t have the definitions of asymptotic stability and stuff. I think I would have to watch some of the earlier lectures in this series for that, maybe I will at some point.
• The Wolfram article
• This Stanford presentation on “Lyapunov theory”
  • This one finally had definitions for G.A.S., L.A.S., etc. (although technically I haven’t seen the definition for trajectory, for example, but I can take a guess).

My Intuitive Understanding

My understanding of Lyapunov functionals is in two pieces:

1. Lyopunov functionals take the issue of convergence/boundedness/other properties in a higher dimensional space by considering convergence/boundedness/other properties in 1D space. We do this through the use of a cleverly constructed functional $V$. Properties of our original trajectory $x$ can be concluded by asking that similar properties hold for the composition $V \circ x$.
2. Lyapunov functionals sort of mimic this idea of “potential energy”. Intuitively, things should go from areas of higher to lower potential, and just like how we have a good idea of how particles move given the equipotential contours, we have a good idea of how the curve should flow given the contours of the Lyapunov functional.

Pretty cool! In the cases of some theorems, the use of Lyapunov functionals and drawing these contours around the convergence points kind of reminds me of null homotopic maps, although I think this relationship is more or less a vague and pointless idea for now. I’ll think about it a bit more, maybe I’ll make another blog post if there really is something interesting there.

Notions of Stability

The idea behind stability is that all “trajectories” converge to the same unique point. If this happens for literally every trajectory, we call it “global asymptotic stability”, or G.A.S., and if this only happens within a certain neighborhood of the limit point $x_e$, we call it “local asymptotic stability”, or L.A.S..

Something else that might be of interest is this (a screenshot taken from the Stanford presentation):

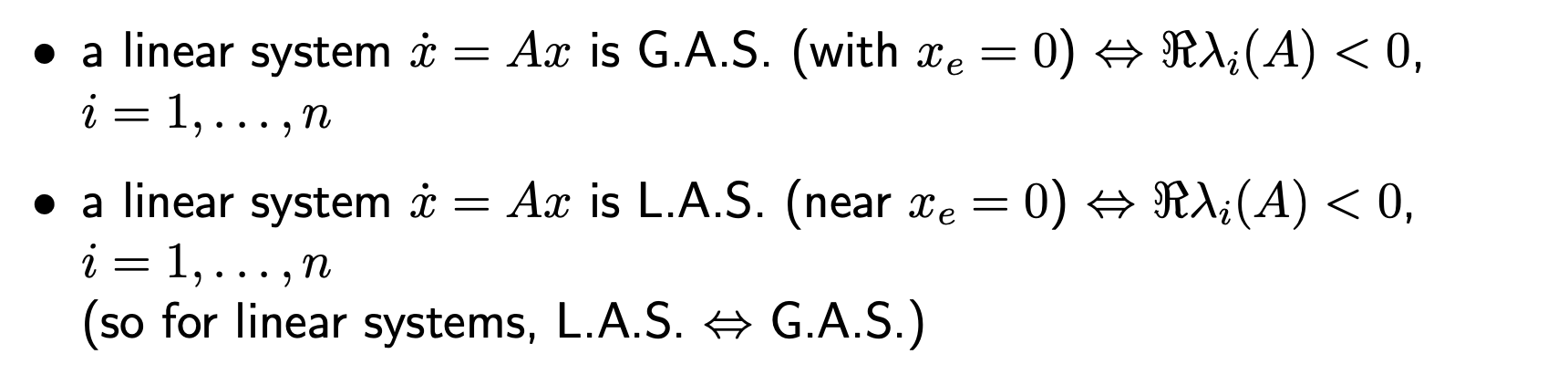
although I’m only 75% sure I know what that weird $\mathfrak{R}\lambda_i$ symbol means. I think $\mathfrak{R}\lambda_i(A)$ means the $i$th eigenvalue of $A$, which would make sense since if all the eigenvalues of the matrix are less than zero, then $\cdot{x}$ will be in a direction “opposite” (sort of) to $x$, so that one might expect $\|x\|$ to get smaller over time. Not totally sure what the $\mathfrak{R}$ means though. Shoot me an email if you know and want to tell me, and I’ll update this post!

The reason for introducing these notions of stability is that we can make Lyapunov theorems that allow us to conclude things about stability if certain Lyapunov functions exist.

Lyapunov Theorems

Now it will be useful to actually define a system. Consider a generic system $\dot{x} = f(x)$ with $f : \R^n \rightarrow \R^n$ a function of $x$ and $x : \R \rightarrow \R^n$ a function of time $t$.

Throughout the following ideas, we will be alluding to “Lyapunov functionals” $V : \R^n \rightarrow \R$. Please note that we will define $\dot{V}$ as $\dot{V} = \nabla V^T f$, so that $\frac{d}{dt}(V \circ x) = \dot{V}$.

According to the Stanford presentation, a typical Lyapunov theorem does the following for us:

• establishes that trajectories of a system satisfy some properties,
• as long as there exists some Lyapunov function $V$ satisfying conditions on $V$ and $\dot{V}$.

Here are some Lyapunov theorems that give us boundedness, GAS, and LAS.

Proof (from the Stanford PDF).

Consider any arbitrary trajectory $x$. If there is a Lyapunov function $V$ with the properties in the second bullet, then for all $t$,

$V(x(t)) - V(x(0)) = \int_0^t \frac{d}{dt}(V\circ x) (s) \; ds = \int_0^t \dot{V}(x) \; ds \le 0.$ In other words, $Vx(t) \le Vx(0)$ for all $t$. So $x(t)$ is in the sublevel set $\{ y : V(y) \le Vx(0)\}$, so $x(t)$ is bounded by the same constant that bounds the sublevel set.

Here are some other results from the Stanford PDF. The proofs are fairly straightforward from the intuitive understanding above.

Proof Sketch. I actually have to do a proof, but in my head, I think this would use Grönwall’s inequality. Intuitively, I’m not actually immediately sure why it was needed that $\alpha > 0$. I’ll have to try the proof.

and more. So far so interesting, I’ll have to try playing around with it more, and maybe I’ll make some notes on it!

See you soon!