ML Low Level Software

January 2, 2026
By Aathreya Kadambi

I’ve been meaning to organize a post on the implementation details of common modeling software such as JAX and PyTorch. These are codebases I’ve always been meaning to explore, but often sacrifice understanding to some extent for immediate practicality. I’ll aim to end that with this post.

Table of Contents

1. PyTorch
   • Tensors
   • Autograd and PyTorch’s Dynamic Computation Graph
   • torch.optim
   • Backends
   • torch.compile [To be continued…]
2. JAX [To be continued…]
   • Tensors
   • Just in Time Compilation
   • Kernel Fusion
   • Devices
3. Notes on GPUs
4. Profiling
   • Speed [To be continued…]
   • Memory [To be continued…]
5. Final Remarks

PyTorch

Tensors

The first big abstraction that PyTorch implements is that of tensors, or multi-dimensional arrays. These are similar to numpy arrays but are GPU-compatible, wheras numpy array methods are designed for CPUs.

Some of the pure awesomeness of PyTorch comes from its ability to magically create accelerated/vectorized CPU code automatically (this crutch should be appreciated rather than abused, cause blackboxing these things leads to future pain). However, one of the main sources of awesomeness of PyTorch in comparison to numpy is its autograd technology.

Autograd and PyTorch’s Dynamic Computation Graph

Tensors can “require grad”, which means that they can keep track their gradients with respect to operations performed on them! One particularly magical line that everyone writes but rarely questions is:

loss.backward()

What is this magical line doing?

In PyTorch, when you compute a tensor from pre-existing tensors, it is a non-leaf tensor. On the contrary, each time you individually define a tensor without computing it from something else in PyTorch, it is a leaf tensor.

When you create a leaf tensor, you can choose to “require grad”, as I mentioned before. Requiring gradients implicitly sparks the creation of a computation graph. Importantly, all operations with PyTorch tensors are combinations of simpler operators which have a “backwards” function. Here is a description of a tensor from the PyTorch docs:

tensor(2.2175, grad_fn=<NegBackward0>)

As you can see, grad_fn is linked to a backwards function “NegBackward0”, which links to a backwards function before it, and so on, through which chain rule can be applied. In other words, through the tensor structure, PyTorch actually keeps track of gradient information through which autograd is performed. For non-leaves that have gradients enabled, generally gradients are not retained, but this behavior can be modified via PyTorch’s retain_grad.

In fact, something people don’t know is that PyTorch can even be used to compute second and higher order gradients. This is something I might try using for more complex mathematical analysis.

torch.nn

PyTorch provides torch.nn, which makes object oriented programming idomatic and implements common neural network layers. This is what most users are very familiar with.

One interesting nuance with torch.nn is that while it provides a great high level framework, it makes many low level choices. For example, note that linear layers use kaiming uniform initialization (see here). Studies have shown that this is a great choice for ReLU networks, but conducting principled work on neural networks means we should continue to inspect and be aware of these choices. Check out this insanely cool Github issue discussion.

I’ll aim to write some code that compares training for simple neural networks with different initalizations and architectures near the end of this post. Interestingly, while PyTorch’s Kaiming initialization has sophisticated consideration of non-ReLU activations, the Linear module doesn’t directly expose this to the user at the time of writing this post.

torch.optim

PyTorch also provides torch.optim, which provides many optimization algorithms such as stochastic gradient descent and Adam.

Backends

PyTorch has a hardware-agnostic API, but internally it actually has different “backends” with math libraries optimized for different devices, such as CPUs, Nvidia GPUs, or Metal GPUs. This is why users select their backend before beginning.

torch.compile

In fact, PyTorch even has a utility to capture computation graphs and compile them into better optimized kernels, just like JAX!

JAX

Overview

Just like PyTorch, JAX also has tensor and autograd functionality. I’ll have to leave it at this, and edit this post later since I’m running out of time according to my schedule.

Devices

One interesting detail with JAX is that while JAX numpy arrays are able to be placed on any device, randomly initialized arrays do not easily include a device parameter. Why?

Profiling

One major concern for software mages is speed and memory overhead of the tools they use. I decided to do some hands on profiling to investigate PyTorch vs. JAX.

Speed

For profiling tools, I want to relive my game programming days and use chrome tracing.

Profiling PyTorch and JAX on linear layers actually shows some interesting results.

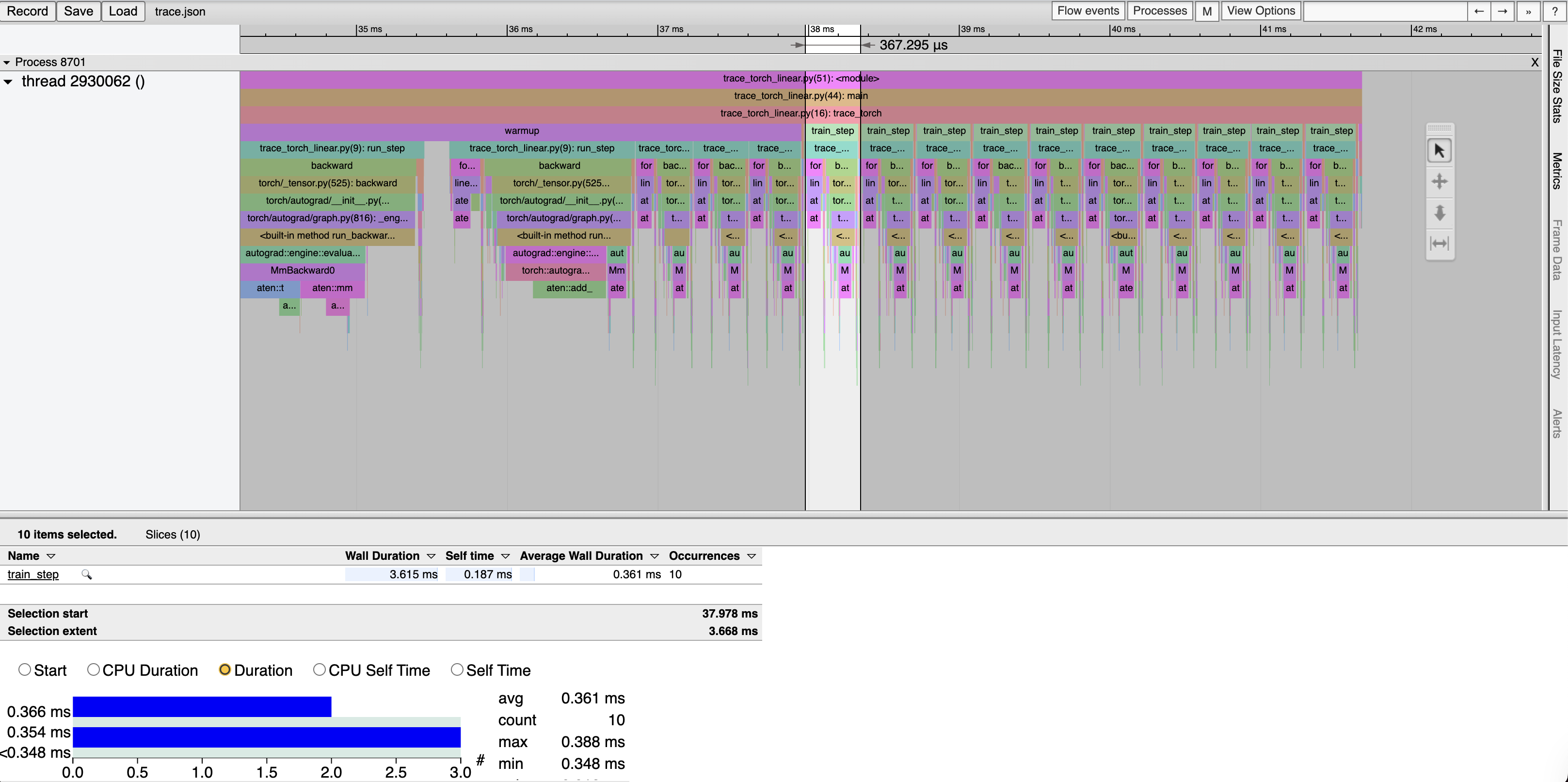
Naive PyTorch Implementation:

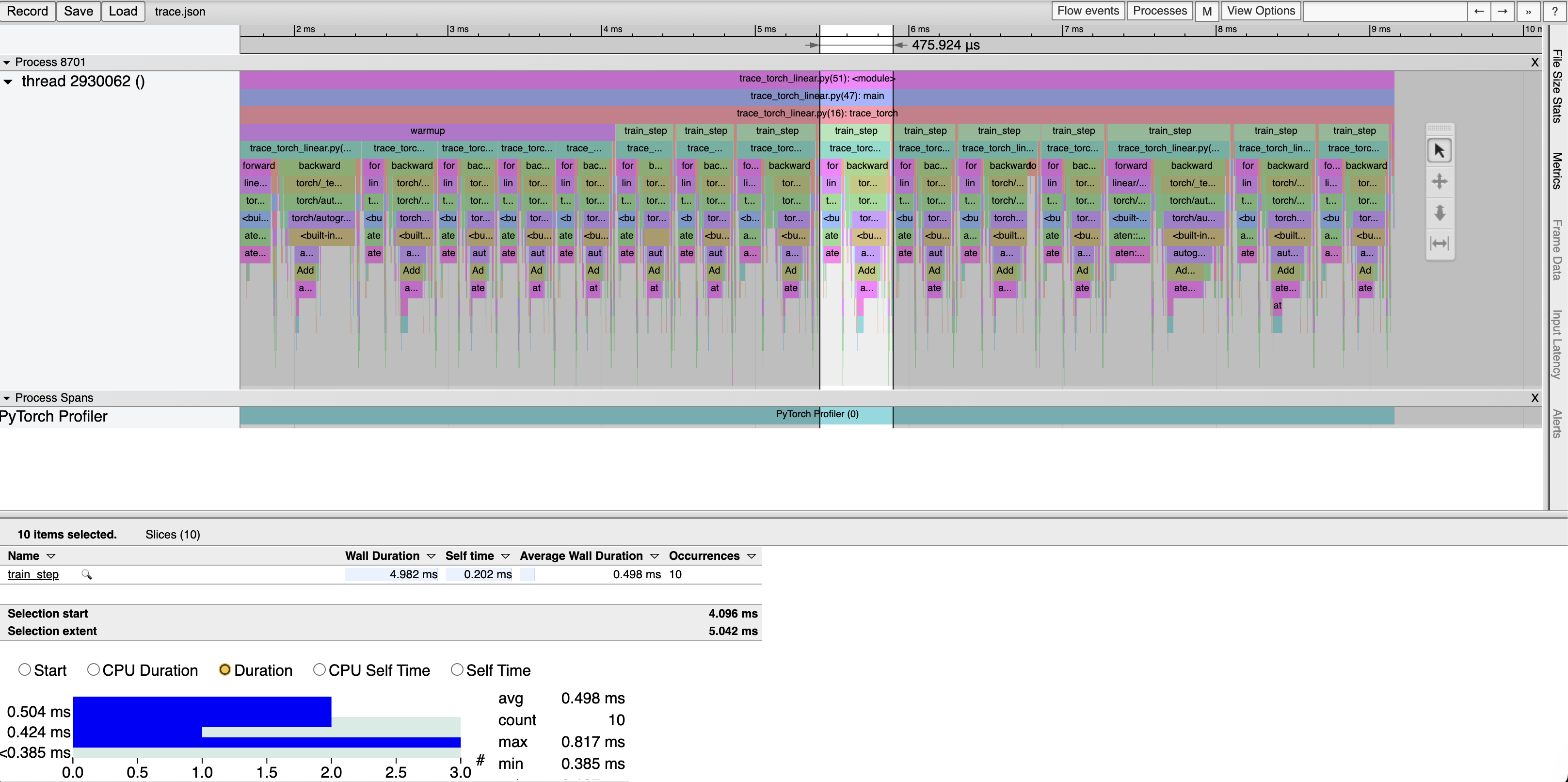
PyTorch’s Linear Layer Implementation:

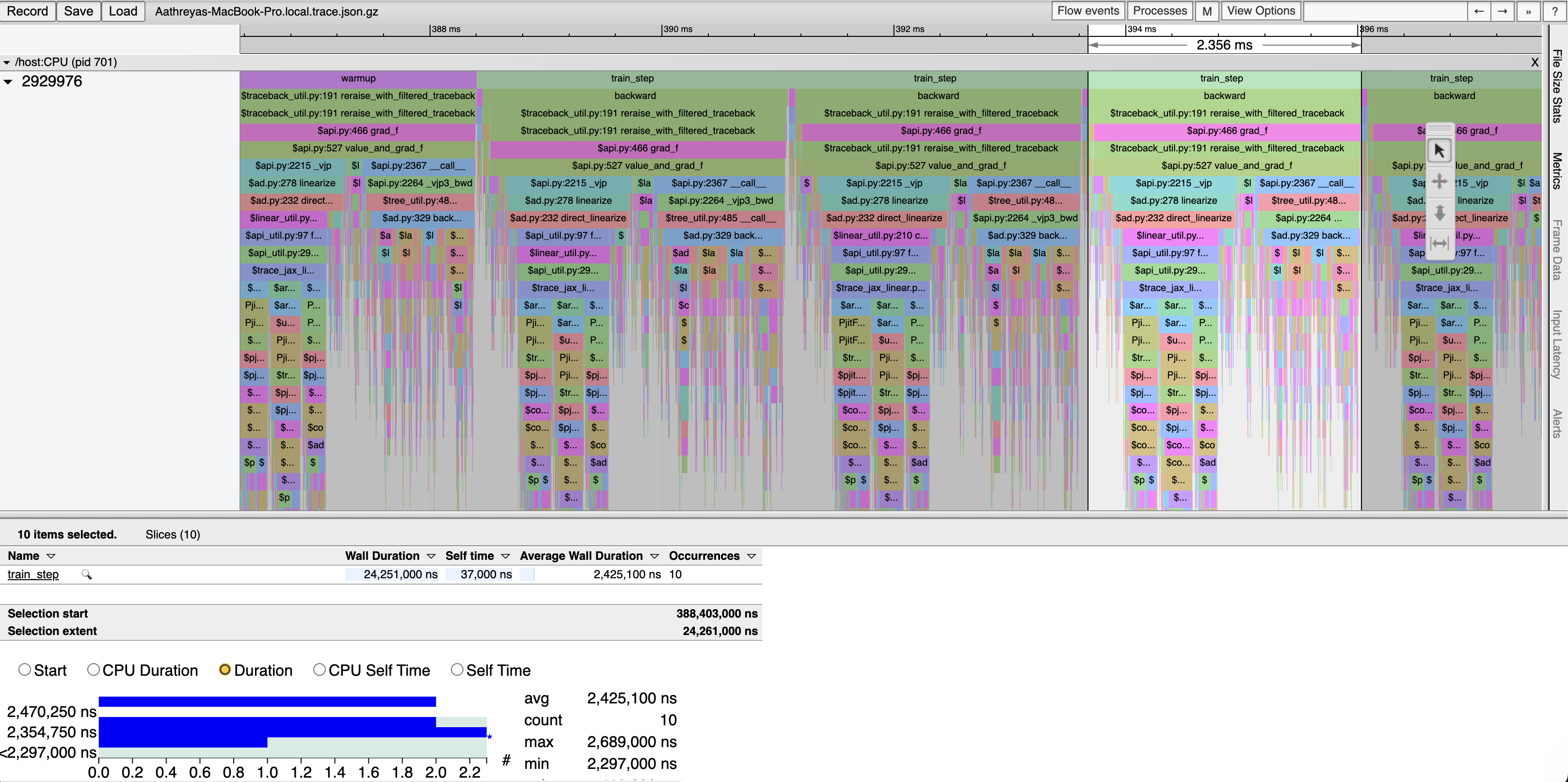
Naive Eager JAX Implementation:

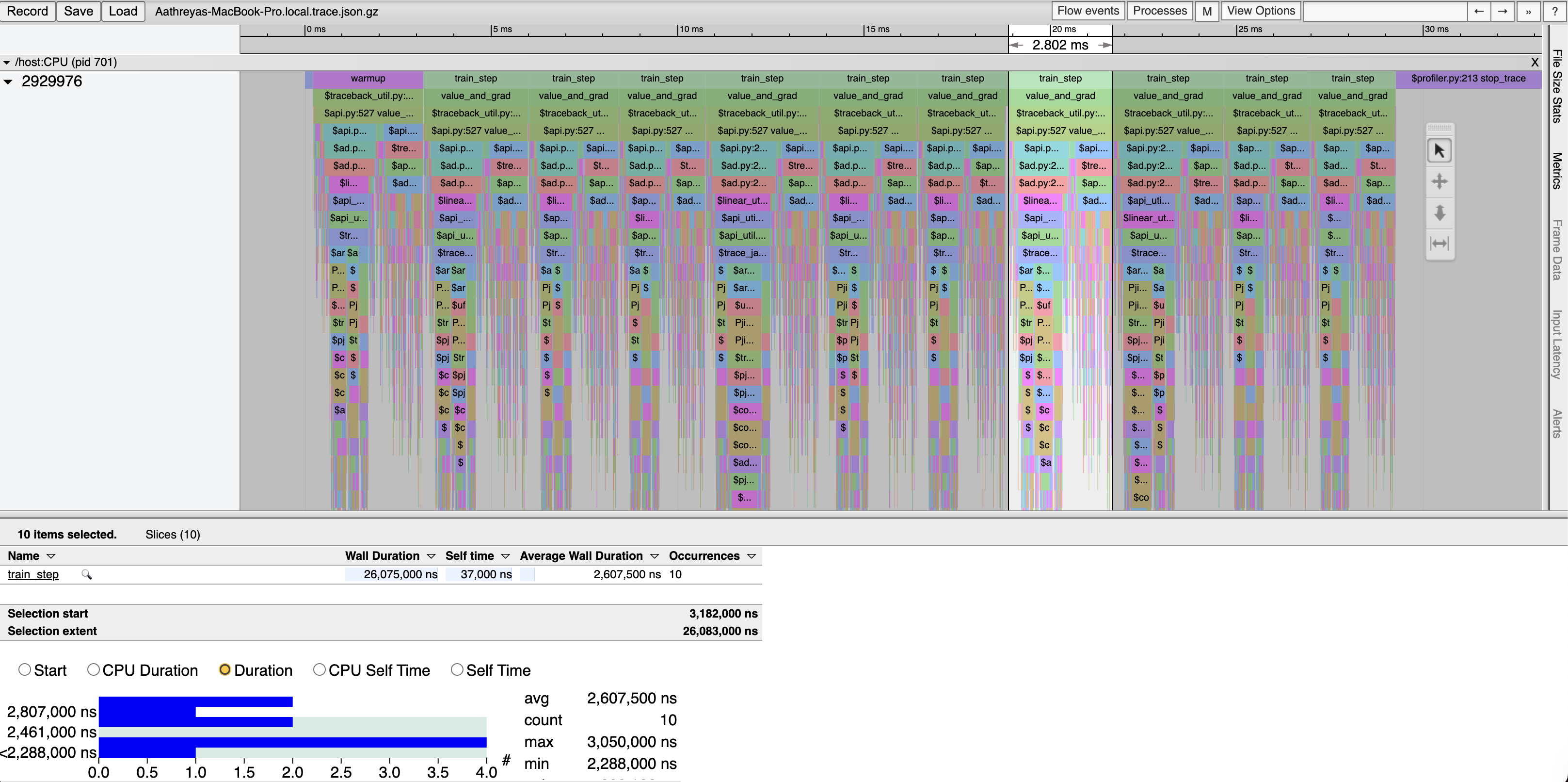
JAX Implementation with value_and_grad:

Naive JIT JAX Implementation:

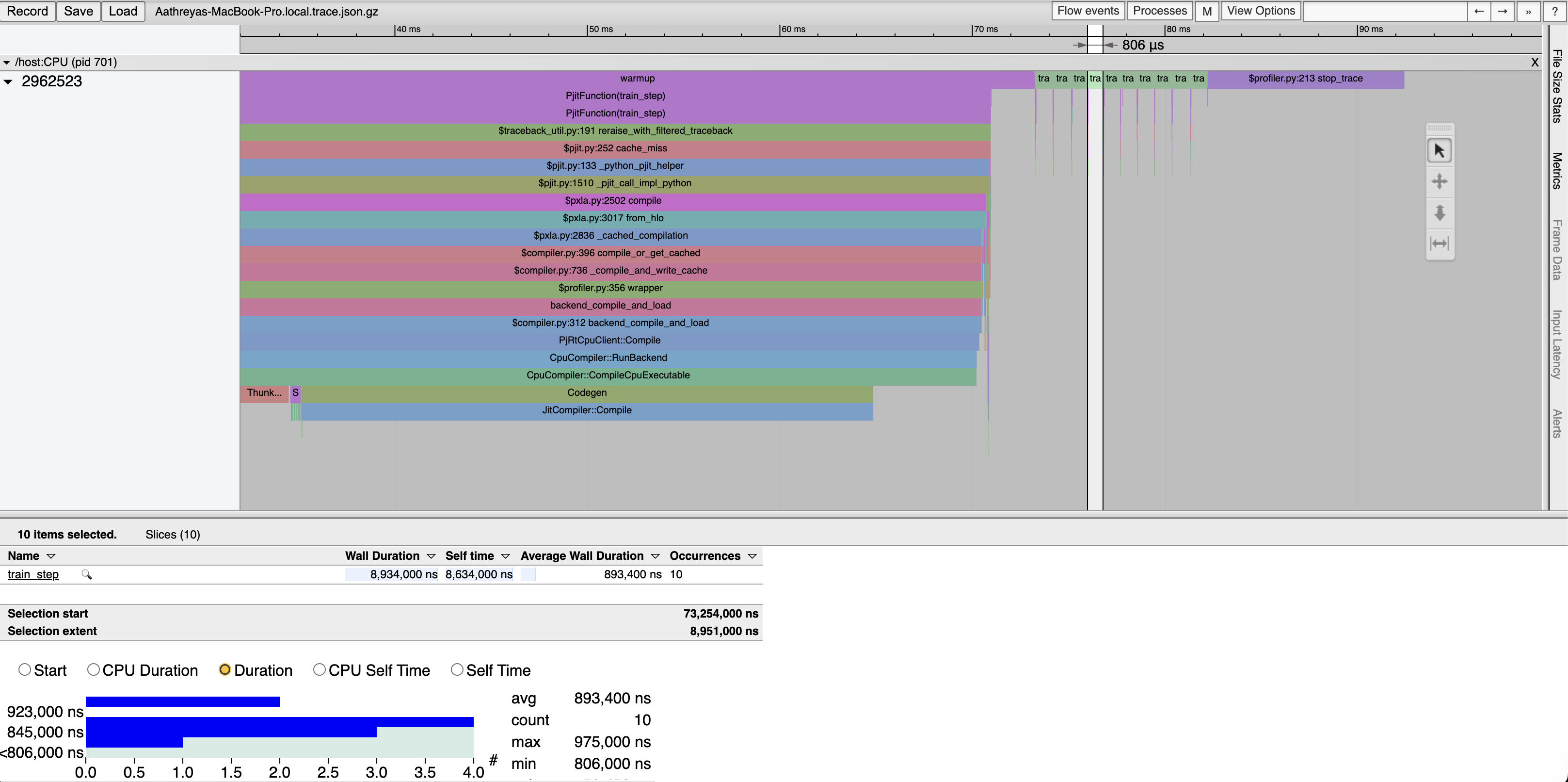
Interestingly, these results show that for linear layers, PyTorch actually outperforms even JIT compiled JAX, after warmup. We also see that naive PyTorch actually tends to be better performing than using PyTorch’s modules, which is unfortunate: PyTorch’s abstractions don’t make easiness correlated with good performance (of course, that is a challenging goal especially for an interpretted language like Python).

Final Remarks

• Found out fast.ai has a great blog: https://www.fast.ai. I might start reading, the posts seem rad. They even have this super cool one with Chris Lattner!
• Loved this: Teleport!